Sometimes, the decoding accuracy of MVPA may lower than chance level, which is confusing. I have found several reasons that may lead to below-chance accuracy in decoding analysis.
- special data structure (bias)
- model parameters (linear vs. non linear)
- cross validation methods (leave-one-out vs. k-fold)
- sample size (small vs. large)
In short, below-chance accuracy is likely caused by data structure and decoding methods, which can not be simply interpreted as anti-learning.
For example, when training with totally random data, the decoding accuracy should fluctuate at the chance level (50%), but actually it may lower than 50%.
library("ggplot2")
library("dplyr")
library("e1071")
# --------training function ---------
f_train <- function(n, s = 1,
r = F, c = n) {
# nv: number of features
nv <- 2
# n: number of observations
set.seed(s)
# generate random data
rNum <- rnorm(nv * n)
rNum <- matrix(rNum, n, nv)
d <- as.data.frame(rNum)
# generate random labels
n2 <- n / 2
labels <- c(array(1, n2),
array(2, n2))
if (r) {
labels <- sample.int(2,n,replace=T)}
else {
labels <- sample(labels)}
d$condition <- factor(labels)
# training
m_trained <- svm(condition ~ .,
data = d,
cross = c,
# cross = nrow(d), # leave one out
kernel = "linear",
cost = 1
)
# get CV
acc <- m_trained$tot.accuracy
}# no replacement, leave one out
p <- expand.grid(iTest = 1:200,
n = seq(10, 210, 50))
data_test <- p %>%
group_by(iTest, n) %>%
do(data.frame(acc = f_train(.$n,.$iTest)))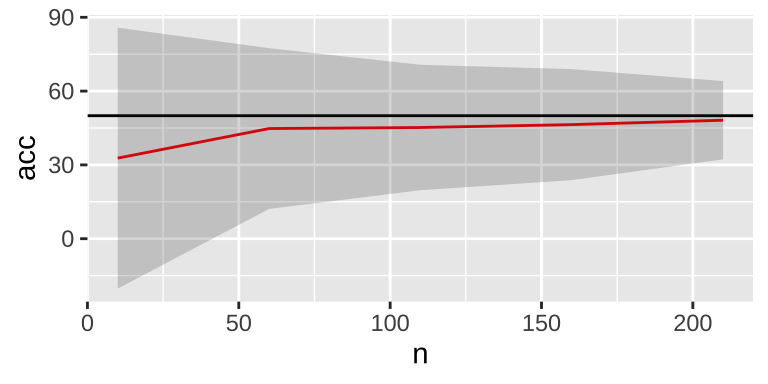
As the sample size increases, variability decreases, and the mean accuracy tends to be 50%. However, there is a persistent small down bias on average, which can be eliminated using sampling with replacement.
# with replacement, leave one out
data_test <- p %>%
group_by(iTest, n) %>%
do(data.frame(acc = f_train(.$n,.$iTest,
r = T)))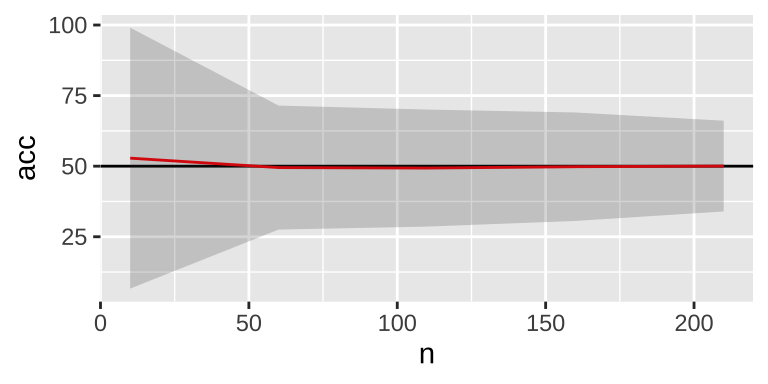
In addition, change to 10-fold cross validation may also decrease the variability.
# with replacement, 10-fold cross validation
data_test <- p %>%
group_by(iTest, n) %>%
do(data.frame(acc = f_train(.$n,.$iTest,
r = F, c=10)))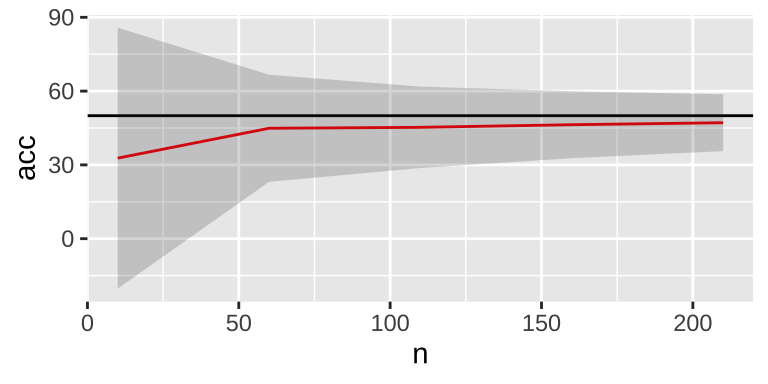
Some references:
- The same analysis approach: Practical protection against the pitfalls of novel neuroimaging analysis methods
- How to control for confounds in decoding analyses of neuroimaging data
- Classification Based Hypothesis Testing in Neuroscience: Below-Chance Level Classification Rates and Overlooked Statistical Properties of Linear Parametric Classifiers
- Multivariate classification of neuroimaging data with nested subclasses: Biased accuracy and implications for hypothesis testing
- Deconstructing multivariate decoding for the study of brain function